Question

WILL MARK THE BRAINILEST!!!!!

Gabby starts to save at age 20 for an extended vacation around the world that she will take on her 40th birthday. She will contribute $250 four times each year to the account, which earns 1.55% annual interest, compounded annually. What is the future value of this investment when she takes her trip?
$23,237.86
$46,684.44
$54,845.69
$93,576.40

Answer 1

Answer: $23,237.86. I just took the test

Answer 2

To solve this we are going to use the compound interest formula with periodic deposits:
`A=P(1+ (r)/(n) )^(nt)+P_(d)( ((1+ (r)/(n))^(nt)-1 )/( (r)/(n) ) )(1+ (r)/(n) )`
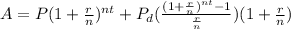
where

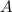
`A` is the final amount after
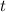
`t` years

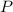
`P` is the initial deposit

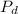
`P_(d)` is the periodic deposit

`r` is the interest rate in decimal form

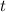
`t` is the time in years

`n` is the number of times the interest is compounded per year

She started to save at age 20, and she is going to save until age 40. We can infer that she is going to save for 20 years. Notice that in the first year, she will open her saving account with $250, and she will make another 3 deposits of $250. Therefore, for her first year:
`P=250`,
`P_(0)=3(250)=750`,
`r= (1.55)/(100) =0.0155`,
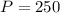
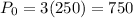
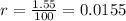
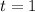
`t=1`, and
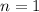
`n=1`. Lets replace those values in our formula:

`A=250(1+ (0.0155)/(1) )^((1)(1))+750( ((1+ (0.0155)/(1))^((1)(1))-1 )/( (0.0155)/(1) ) )(1+ (0.0155)/(1) )`

`A=250(1.0155 )+750( ((1.0155)-1 )/( 0.0155 ) )(1.0155)`

`A=1015.5`

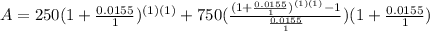
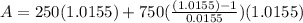
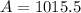
Now, for the next 19 years the initial amount in Gabby's account will be $1015.5; therefore,
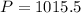
`P=1015.5`. We can also infer that
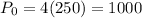
`P_(0)=4(250)=1000` and
`t=19`. We also know from previous calculations that
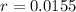
`r=0.0155`, and
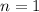
`n=1`. So lets replace those values in our formula one more time:

`A=P(1+ (r)/(n) )^(nt)+P_(d)( ((1+ (r)/(n))^(nt)-1 )/( (r)/(n) ) )(1+ (r)/(n) )`

`A=1015.5(1+ (0.0155)/(1) )^((1)(19))+1000( ((1+ (0.0155)/(1))^((1)(19))-1 )/( (0.0155)/(1) ) )(1+ (0.0155)/(1) )`

`A=1015.5(1.0155 )^(19)+1000( ((1.0155)^(19)-1 )/(0.0155 ) )(1.0155 )`

`A=23598.04`

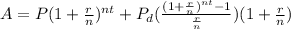
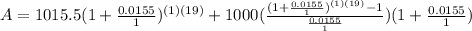
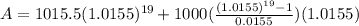
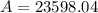
We can conclude that the future value of her investment when she takes her trip is $23,598.04.