Question

Suppose the surface area of a sphere is 324π square units. What is the volume, in cubic units, of this sphere

A) 9π
B) 81π
C) 324π
D) 972π

Answer 1

D would be the answer

Answer 2

Option D is correct

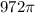`972 \pi` is the volume, in cubic units, of this sphere

Explanation:

Surface area of sphere(S) and volume of sphere (V) is given by:

`S = 4 \pi r^2`

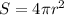
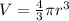`V = (4)/(3) \pi r^3` .....[1]

As per the statement:

Suppose the surface area of a sphere is 324π square units

⇒S = 324π square units

then;

`324 \pi = 4 \pi r^2`

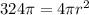
Divide both side by
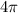`4 \pi` we have;

`81 = r^2`

or

`r^2= 81`

⇒
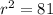
`r = √(81) = 9` units

We have to find the volume, in cubic units, of this sphere.

Substitute the given value in [1] we have;

`V = (4)/(3) \pi \cdot 9^3 = (4)/(3) \pi \cdot 729`

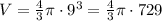
Simplify:

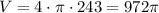`V = 4 \cdot \pi \cdot 243 = 972 \pi` cubic units

Therefore,
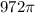`972 \pi` is the volume, in cubic units, of this sphere