Question

Mia records the distance traveled in x minutes in the table below, while Alexa uses a graph to record her distance traveled over the same time period. (look at the graphs)

Based on the data on the graph and in the table, which statement gives an accurate comparison?
Alexa traveled at a faster rate because the slope of her line is 3/4 , which is greater than the slope of the line described by the data in Mia’s table.
Alexa traveled at a faster rate because the slope of her line is4/3 , which is greater than the slope of the line described by the data in Mia’s table.
Mia traveled at a faster rate because the slope of the line described by the data in her table is 1/2 , which is greater than the slope of the line on Alexa’s graph.
Mia traveled at a faster rate because the slope of the line described by the data in her table is 2/1 , which is greater than the slope of the line on Alexa’s graph.

Answer 1

Answer: The correct option is

(A) Alexa travelled at a faster rate because the slope of her line is
`(3)/(4)`, which is greater than the slope of the line described by the data in Mia’s table.

Step-by-step explanation: Given that Mia records the distance travelled in x minutes in the table below, while Alexa uses the given graph to record her distance travelled over the same time period.

We are to select the accurate comparison based on the data on the graph and in the table.

We know that the slope of a line passing through the points (a, b) and (c, d) is given by

`m=(d-b)/(c-a).`

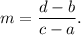
For Alexa's graph :

From the graph, we note that the straight line passes through the points (4, 3) and (8, 6).

Therefore, the slope of the line on the graph will be

`m_1=(6-3)/(8-4)\\\\\\\Rightarrow m_1=(3)/(4).`

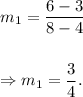
For Mia's table :

From the table, we see that two of the points are (10, 5) and (18, 6).

Therefore, the slope of the line described by the table is given by

`m_2=(9-5)/(18-10)\\\\\\\Rightarrow m_2=(4)/(8)\\\\\\\Rightarrow m_2=(1)/(2).`

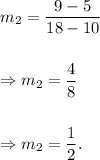
Now, we have

`(1)/(2)=(2)/(4)<(3)/(4)\\\\\\\Rightarrow (3)/(4)>(1)/(2)\\\\\Rightarrow m_1=m_2.`

So, the slope of Alexa's graph is greater than the slope of Mia's table. This implies that Alexa travelled at a faster rate than Mia.

Hence, Alexa travelled at a faster rate because the slope of her line is
`(3)/(4)`, which is greater than the slope of the line described by the data in Mia’s table.

Option (A) is CORRECT.

Answer 2

1. Alexa traveled at a faster rate because the slope of her line is
`(3)/(4)`, which is greater than the slope of the line described by the data in Mia’s table.

Explanation:

We know that,

Slope of
`(x_(1),y_(1))` and
`(x_(2),y_(2))` is
`(y_(2)-y_(1))/(x_(2)-x_(1))`

Mia records the distance traveled over the time by the table.

Taking the points (10,5) and (18,9), the slope is given by,

Mia's slope =
`(9-5)/(18-10)`

i.e. Mia's slope =
`(4)/(8)`

i.e. Mia's slope =
`(1)/(2)`

Alexa records the distance traveled over the time by the graph.

Taking the points (4,3) and (8,6), the slope is given by,

Alexa's slope =
`(6-3)/(8-4)`

i.e. Alexa's slope =
`(3)/(4)`

As, Alexa's slope =
`(3)/(4)` >
`(1)/(2)` = Mia's slope.

So, the correct option is,

1. Alexa traveled at a faster rate because the slope of her line is
`(3)/(4)`, which is greater than the slope of the line described by the data in Mia’s table.