Question

HELP 
Which equations represent hyperbolas?

Answer 1

An elliptical equation is in the form
Ax^2+Bx+Cy^2+Dy+E=0
the equation is a Hyperbola. When x and y are both squared, and exactly one of the coefficients is negative and exactly one of the coefficients is positive.
1-49x^2-98x-64y^2+256y-2831=0
2-4x^2+32x-25y^2-250y+589=0
3-81x^2+512x-64y^2-324y-3836=0

Answer 2

Answer: The required equations of hyperbolas would be

`49x^2-98x-64y^2+256y-2831=0\\\\4x^2+32x-25y^2-250y+589=0\\\\81x^2+512x-64y^2-324y-3836=0`

Explanation:

Since we know that

The general equation for a conic section:

`Ax^2+Bxy+Cy^2+Dx+Ey+F=0`

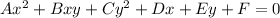
In case of hyperbola, we get that

`Discriminant=B^2-4AC>0`

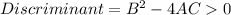
According to this, both x and y are squared.

And one of the coefficient of x and y must be positive and one of the coefficient of x and y must be negative.

So, the required equations of hyperbolas would be

`49x^2-98x-64y^2+256y-2831=0\\\\4x^2+32x-25y^2-250y+589=0\\\\81x^2+512x-64y^2-324y-3836=0`