Question

A particle moves along the parabolic path given by y^2=4x in such a way that when it is at the point (1,-2), its horizontal velocity (in the direction of the x-axis) is 3ft/s. What is its vertical velocity (in the direction of the y-axis) at this instant? PLEASE SHOW WORK AND ANSWER IN THE COMMENTS!

Answer 1

The particle's position as a function of time is parameterized by the ordered pair of functions
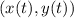
`(x(t),y(t))`, with


`y(t)^2=4x(t)`

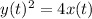
If we differentiate both sides of this equation with respect to time
`t`, we have


`2y(t)(\mathrm dy(t))/(\mathrm dt)=4(\mathrm dx(t))/(\mathrm dt)`

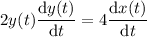
where the derivatives of
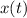
`x(t)` and
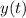
`y(t)` represent change in horizontal and vertical position, respectively, over time. In other words, these are the particle's horizontal/vertical velocities.

We're told that the horizontal velocity at a certain point in time - namely, when the particle's position is (1, -2) - is 3 ft/s, which is to say that at some time
`t`, we have


`2(-2)(\mathrm dy(t))/(\mathrm dt)=4(3)\implies(\mathrm dy(t))/(\mathrm dt)=-3`

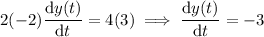
In other words, under the given conditions, the particle has a downward vertical velocity of 3 ft/s.