Question

Can anyone explain how to do this? it's graphing tangent and cotangent

Answer 1

I don't see an equation with cotangent but I can graph
`y=-\tan\left(\frac{\pi x}4\right)`.

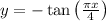
The input of the tangent function is multiplied by
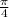
`\frac{\pi}4`. Normally, the tangent function has asymptotes at
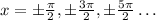
`x=\pm\frac{\pi}2,\pm\frac{3\pi}2,\pm\frac{5\pi}2\ldots`. Instead, each of these aymptotes will be divided by
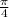
`\frac{\pi}4` (when the input is multiplied, the known x values are divided). That means the new function has asymptotes at
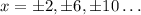
`x=\pm2,\pm6,\pm10\ldots`. The new function's period is 4.

Normally, the slope of the tangent function is 1 at 0, and whenever it crosses the x axis. Your function is negative, so instead of drawing from negative infinity to infinity with a positive slope when it intersects 0, draw from positive infinity to negative infinity with a negative slope when it intersects 0.