Question

A ladder that is 26 feet long leans against a building, making a 65 degree angle of elevation with the ground.

To the nearest tenth of a foot, how far up the building does the ladder reach?
A) 11.0 ft
B) 12.1 ft
C) 23.6 ft
D) 28.7 ft

Answer 1

Explanation:

I took the quiz :)

Answer 2

C) 23.6 ft.

Explanation:

Please find the attachment.

Let h be the length of building that could be reached by ladder.

We have been given that a ladder that is 26 feet long leans against a building, making a 65 degree angle of elevation with the ground.

We can see from our attachment that the length of the ladder and the building forms a right triangle with respect to ground.

The length of ladder is hypotenuse and the height of building (h) is the opposite side of right triangle.

Since we know that trigonometric ratio Sine represents the relation between opposite and hypotenuse of right triangle.

`\text{Sin}=\frac{\text{Opposite}}{\text{Hypotenuse}}`

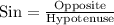
Upon substituting our given values in above equation we will get,

`\text{Sin}(65^o)=(h)/(26)`

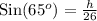
Let us multiply both sides of our equation by 26.

`\text{Sin}(65^o)*26=(h)/(26)*26`

`\text{Sin}(65^o)*26=h`

`0.906307787037*26=h`

`23.564002462962=h`

`h\approx 23.6`

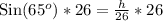
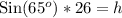
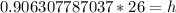
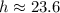
Therefore, the ladder will reach the building up to 23.6 ft and option C is the correct choice.