Question

What is the sum of the first 10 terms of the sequence defined by an=3n-3?

Answer 1

The answer is D. 135

Answer 2

The sum of first 10 terms of the sequence defined by
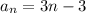`a_n=3n-3` is 135.

Explanation:

Given : nth term of a sequence as
`a_n=3n-3`

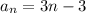
We have to find the sum of first 10 terms of the sequence.

Consider the nth term of a sequence as
`a_n=3n-3`

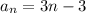
Then put n = 1 to get the first term

`a_1=3(1)-3=0`

put n = 2 to get the next term

`a_2=3(2)-3=6-3=3`

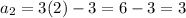
put n = 3 to get the next term

`a_3=3(3)-3=9-3=6`

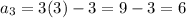
put n = 4 to get the next term

`a_4=3(4)-3=12-3=9`

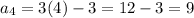
Thus, the sequence is of the form 0, 3, 6, 9,.....

Thus, the above is an arithmetic sequence with a = 0 and common difference (d) = 3

Thus, Sum of 10 terms is given by

`S_n=(n)/(2)(2a+(n-1)d)`

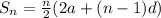
n = 10 , a = 0 , d = 3

Put we get,

`S_(10)=(10)/(2)(2(0)+(10-1)3)`

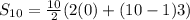
Simplify, we have,

`S_(10)=5(9* 3)`

`S_(10)=135`

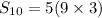
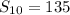
Thus, the sum of first 10 terms of the sequence defined by
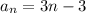`a_n=3n-3` is 135.