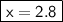Perimeter is the sum of all the sides. So we can set up an equation:
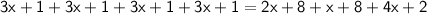
Now solve for 'x', combine like terms:
When it comes to terms with variables it's just like normal addition but we keep the variable:
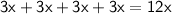
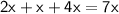
So we have:
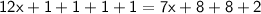
Add:
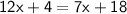
Subtract 7x to both sides:
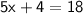
Subtract 4 to both sides:
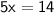
Divide 5 to both sides: