Question

What is the graph of the function f(x)= f(x)=-x^2-9x-20/x+4?

Answer 1

Synthetic division? You’ll make the positive 4 a negative then set it up as a long division except you only put the numbers and not the x’s. So it would be -4 division sign then on the right of the line is -1 -9-20. Then you bring the -1 down and multiply -4 by -1 which would be 4 and you put it under -9 then do the simple math for those then bring the -5 down to the right of the negative 1. Then multiply negative 4 by negative 5 which is positive 20. So your answer wouldn’t have a remainder. So it would be -x-5

Answer 2

Graph in attachment

Explanation:

Given:
`f(x)=(-x^2-9x-20)/(x+4)`

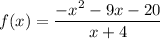
We need to draw the graph of rational function f(x).

First we find the x and y intercept of f(x)

For x-intercept: put f(x)=0

`(-x^2-9x-20)/(x+4)=0`

`-x^2-9x-20=0`

`(x+5)(x+4)=0`

`x=-5`

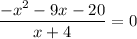
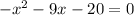
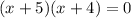
For y-intercept: Put x=0

`f(0)=(0^2-9\cdot0-20)/(0+4)`

`f(0)=-5`

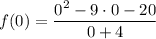
For vertical asymptote: Set denominator to 0

`x+4=0`

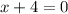
But x+4 is common factor at numerator and denominator.

So, x=-4 will be hole of the graph.

Hole: x=-4

Using above information to draw the graph.

Please find attachment for graph.