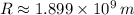Answer:
The radius of its orbit is
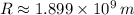 .
.
Step-by-step explanation:
Let suppose that Callisto rotates around Jupiter in a circular path and at constant speed, then we understand that net acceleration of this satellite is equal to the centripetal acceleration due to gravity of Jupiter. That is:
 (1)
(1)
Where:
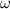 - Angular speed, measured in radians per second.
- Angular speed, measured in radians per second.
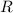 - Radius of the orbit, measured in meters.
- Radius of the orbit, measured in meters.
 - Net acceleration, measured in meters per square second.
- Net acceleration, measured in meters per square second.
In addition, angular speed can be described in terms of period (
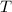 ), measured in seconds:
), measured in seconds:
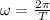 (2)
(2)
And the net acceleration by the Newton's Law of Gravitation:
 (3)
(3)
Where:
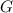 - Gravitation constant, measured in cubic meters per kilogram-square second.
- Gravitation constant, measured in cubic meters per kilogram-square second.
 - Mass of Jupiter, measured in kilograms.
- Mass of Jupiter, measured in kilograms.
Now we apply (2) and (3) in (1) to derive an expression for the radius of the orbit:
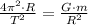
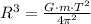
![R = \sqrt[3]{(G\cdot m\cdot T)/(4\pi^(2)) }](https://img.qammunity.org/2022/formulas/physics/high-school/5s0cslqzrnnoaq186x2zgt1zeiorx0gutw.png) (4)
(4)
If we know that
 ,
,
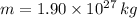 and
and
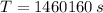 , then the radius of the orbit of Callisto is:
, then the radius of the orbit of Callisto is:
![R = \sqrt[3]{((6.674* 10^(-11)\,(m^(3))/(kg\cdot s^(2)) )\cdot (1.90* 10^(27)\,kg)\cdot (1460160\,s)^(2))/(4\pi^(2)) }](https://img.qammunity.org/2022/formulas/physics/high-school/sh7wwp6qlt5vwgd4nsiusgup7datx9r6ri.png)