Question

The linear function that is represented by which table has the same slope as the graph? (the tables are the choices)

Answer 1

Answer: is

( C )

Explanation:

Answer 2

Answer with explanation:

Slope between two points having coordinates,
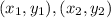`(x_(1),y_(1)),(x_(2),y_(2))` which lie in a coordinate plane is given by:

`=(y_(2)-y_(1))/(x_(2)-x_(1))`

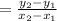
1.. Slope of linear function given in table 1, can be calculated by

`=(-7-(-9))/(-21-(-25))\\\\=(2)/(-21+25)\\\\=(2)/(4)\\\\=(1)/(2)`

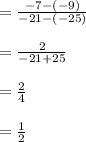
2. Slope of linear function given in table 2, can be calculated by

`=(7-9)/(-21-(-25))\\\\=(-2)/(-21+25)\\\\=(-2)/(4)\\\\=(-1)/(2)`

3. Slope of linear function given in table 3, can be calculated by

`=(-21-(-25))/(-7-(-9))\\\\=(-21+25)/(-7+9)\\\\=(4)/(2)\\\\=(2)/(1)=2`

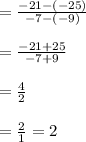
4. Slope of linear function given in table 3, can be calculated by

`=(-13-(-9))/(3-1)\\\\=(-4)/(2)\\\\=(-2)/(1)\\\\=-2`

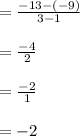
→Now, slope of line which passes through (0,-3) and (3,3) is

`=(3-(-3))/(3-0)\\\\=(6)/(3)\\\\=2`

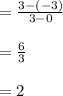
→→→Table 3,

x : -9 -7 -5 -3 -1

y: -25 -21 -17 -13 -9

has same slope as line given equal to 2.