Question

Smallest Zero of f(x+5)=x^2+3x+30

Answer 1

The zeros of
`x^2+3x+30` can be obtained by the quadratic formula (we use this method because the function is not factorable and has no real solutions, so it is easiest).

For a general quadratic
`ax^2+bx+c=0`,


`x= (-b \pm √(b^2-4ac) )/(2a)`.

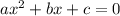
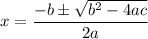
For our function, a = 1, b = 3, and c = 30.

We substitute and solve for x:


`=(-(3) \pm √((3)^2-4(1)(30)) )/(2(1))= (-3 \pm √(9-120) )/(2)\\\\\\= (-3 \pm √(-111) )/(2)=(-3 \pm i√(111) )/(2)`


`x=(-3+i √(111))/(2) \ \\\\\\\ x = (-3-i √(111))/(2) \`

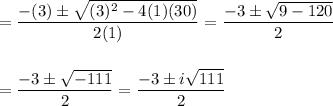
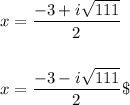
The modulus of each complex solution is about 5.477, so neither solution is bigger or smaller.

Answer 2

Hey there
_________________
The correct answer is:
f(x+5)=(x+5)^2+3(x+5)-10

f(x+5)=x^2+10x+25+3x+15-10

f(x+5)=x^2+13x+30 and f(x+5)=x^2+kx+30 so

k=13

Now factor x^2+13x+30

Find j and k such that jk=ac=30 and j+k+b=13 so j and k are 10 and 3 so

(x+3)(x+10)

So the two zeros occur when x=-3 and -10 the smallest of which is:

x=-10

___________________________
Hope this helps you