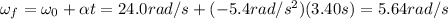Question

A spinning wheel is slowed down by a brake, giving it a constant angular acceleration of −5.40 rad/s2. during a 3.40-s time interval, the wheel rotates through 50.4 rad. what is the angular speed of the wheel at the end of the 3.40-s interval?

Answer 1

The law of motion for the wheel is

`\theta(t)= \omega_0 t + (1)/(2) \alpha t^2`
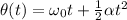
where

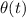
`\theta(t)` is the angle covered after a time interval t

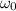
`\omega _0` is the initial angular speed of the wheel

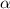
`\alpha` is the angular acceleration of the wheel

We know that after a time t=3.40 s the angle covered by the wheel is 50.4 rad, so we can use these data and re-arrange the previous formula to find the initial angular speed:

`\omega_0 = (\theta - (1)/(2)\alpha t^2 )/(t)= (50.4 rad - (1)/(2)(-5.40 rad/s^2)(3.40 s)^2 )/(3.40 s)= 24.0 rad/s`

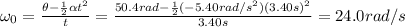
And then, the final angular speed will be given by

`\omega_f = \omega_0 + \alpha t=24.0 rad/s +(-5.4 rad/s^2)(3.40 s)=5.64 rad/s`