Question

The number of cans xavier recycled each week for eight weeks is 24,33.76,42,35,33,44,and 33.find the mean, median, range iqr, and standard deviation of the data. is any value an outlier? if so, which value? 10-4 answer key

Answer 1

The mean is 40; the median is 34; the range is 52; the interquartile range is 52; the standard deviation is 41.8; and 76 is an outlier.

Step-by-step explanation:
To find the mean, find the sum of all data points and divide by the number of data points, 8:

24+33+33+33+35+42+44+76 = 320/8 = 40

To find the median, list the data in order from least to greatest and find the middle value. The middle will be between 33 and 35; averaging these two numbers,

(33+35)/2 = 34.

To find the interquartile range, we first find the Upper Quartile and Lower Quartile. This means we find the median of the upper half of the data; this is between 42 and 44:

(42+44)/2 = 43

We also find the median of the lower half of the data; this is between 33 and 33, so it is 33.

The interquartile range is 43-33=10.

To find the standard deviation, we subtract the mean from each data point, square it, add them together and find the square root:


`\sigma=√((-16)^2+(-7)^2+(-7)^2+(-7)^2+(-5)^2+(2)^2+(4)^2+(36)^2) \\ \\=\sqt{256+49+49+49+25+4+16+1296}=√(1744)=41.8`

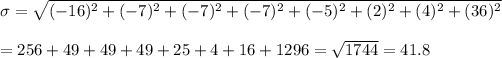
To determine if a number is an outlier, we find any numbers 1.5 times the IQR below the lower quartile or any numbers 1.5 times the IQR above the upper quartile:

1.5(10) = 15
43+15 = 58; 76 is an outlier;
33-15 = 18; no lower outliers.