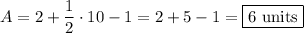You can use Pick's theorem, where:
Area = Number of interior points (points inside the polygon) +

· Number of boundary points (points on the polygon's perimeter) - 1
so:
1.Yellow:
Interior points = 3
Boundary points = 8
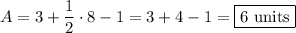
2. Red:
Interior points = 2
Boundary points = 10