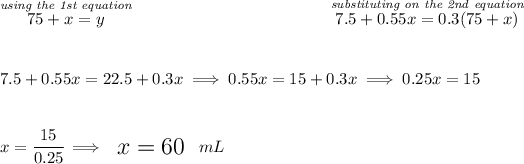Question

You need a 30% alcohol solution. On hand, you have a 75 mL of a 10% alcohol mixture. You also have 55% alcohol mixture. How much of the 55% mixture will you need to add to obtain the desired solution?

Answer 1

A = 10% alcohol solution

B = 55% alcohol solution

we know we have 75 mL of A, that means A itself since it's 10% alcohol, really only has 75 * (10/100) = 7.5 mL of alcohol, likewise the B solution has say "x" mL, so alcohol wise it only has "x" * (55/100) = 0.55x, and we have a final mixture we need of say "y" mL at 30% alcohol.

`\begin{array}{lcccl} &\stackrel{solution}{quantity}&\stackrel{\textit{\% of }}{amount}&\stackrel{\textit{mL of }}{amount}\\ \cline{2-4}&\\ A&75&0.10&7.5\\ B&x&0.55&0.55x\\ \cline{2-4}&\\ mixture&y&0.30&0.3y \end{array}~\hfill \begin{cases} 75+x=y\\\\ 7.5+0.55x=0.3y \end{cases} \\\\[-0.35em] ~\dotfill`
`\stackrel{\textit{using the 1st equation}}{75+x=y}\hspace{12em}\stackrel{\textit{substituting on the 2nd equation}}{7.5+0.55x=0.3(75+x)} \\\\\\ 7.5+0.55x=22.5+0.3x\implies 0.55x=15+0.3x\implies 0.25x=15 \\\\\\ x=\cfrac{15}{0.25}\implies {\Large \begin{array}{llll} x=60 \end{array}} ~mL`