Answer:
event 2 > event 4> event 1> event 2
Explanation:
Probability of getting an event =
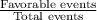
Total outcomes of rolling a dice twice = 36
{1,1};{1,2};{1,3};{1,4};{1,5};{1,6}
{2,1};{2,2};{2,3};{2,4};{2,5};{2,6}
{3,1};{3,2};{3,3};{3,4};{3,5};{3,6}
{4,1};{4,2};{4,3};{4,4};{4,5};{4,6}
{5,1};{5,2};{5,3};{5,4};{5,5};{5,6}
{6,1};{6,2};{6,3};{6,4};{6,5};{6,6}
1)The probability of getting the same number on each roll.
Favorable events : {1,1};{2,2};{3,3};{4,4};{5,5};{6,6} = 6
So, probability of getting the same number on each roll=
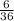
2)the probability of obtaining an odd prime number (excluding 1) on each roll.
Favorable events : {3,3};{3,5};{5,3};{5,5} = 4
So, the probability of obtaining an odd prime number (excluding 1) on each roll =
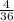
3)the probability that the difference of the two numbers is at most 1.
So, we are supposed to find the probability of getting the number whose the difference is less than or equal to 1
Favorable events : {1,1};{1,2};{2,1};{2,2};{2,3};{3,2};{3,3};{3,4};{4,3};{4,4};{4,5};{5,4};{5,5};{5,6};{6,5};{6,6} =16
So, the probability that the difference of the two numbers is at most 1 =
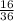
4)the probability that the second number is a multiple of the first number
Favorable events : {1,1};{1,2};{1,3};{1,4};{1,5};{1,6};{2,2};{2,4};{2,6};{3,3};{3,6};{4,4};{5,5};{6,6}=14
So, the probability that the second number is a multiple of the first number =
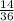
Probabilities in decreasing order :
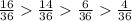
The event with the highest probability to the event with the lowest probability : event 2 > event 4> event 1> event 2
Hence , the events in order from the event with the highest probability to the event with the lowest probability is event 2 > event 4> event 1> event 2