Answer:
The measure of ∠RST=15°
A is correct.
Explanation:
Given: Circle with centre H. Radius of circle is 6 cm.
Length of minor arc
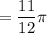
RS ≅ TS (Given)
arc RS = arc ST ( equal choed subtended equal arc.
Major arc RT
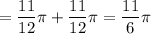
Minor arc RT
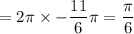
Central angle of minor arc = ∠RHT
Therefore,
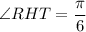
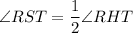
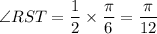
Now we will change radian to degree
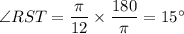
Hence, The measure of ∠RST=15°