Question

In equilateral ΔABC, AD, BE, and CF are medians. If FO = 4, then AE = A) 4 B) 4 3 C) 8 D) 12

Answer 1

Your answer choice would be C) 8.

Explanation:

Answer 2

Firstly, we need to draw triangle

we know that

O is a centroid

and centroid divides median into 2:1

so,

`(CO)/(FO) =(2)/(1)`

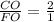
we have FO=4

so, we can plug it

`(CO)/(4) =(2)/(1)`

`CO=8`

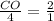
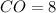
now, we can find CF

CF=OC+FO

CF=8+4

CF=12

now, we can see triangle ACF is a right angled triangle

so, we can use pythagoras theorem

`x^2=((x)/(2) )^2+12^2`

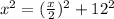
now, we can solve for x

`(3x^2)/(4)=144`

`x^2=192`

`x=8√(3)`

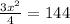
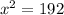
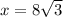
Since, it is equilateral triangle

so,

`AC=x=8√(3)`

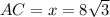
we know that

E is a mid-point

so,

`AE=(AC)/(2)`

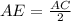
now, we can plug values

`AE=(8√(3))/(2)`

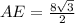
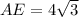`AE=4√(3)`................Answer