Question

Kendall bought 3 glazed donuts and 3 filled donuts and they fit perfectly in the 9" by 6" box. What is the area of the bottom of the box (the shaded region) not covered by donuts?

answer all questions

Answer 1

yes

Explanation:

Answer 2

The area of the bottom of the box (the shaded region) not covered by donuts will be 13.94 in²

Explanation

1. Across the length of the box, there are three filled donuts. That means the total diameter of three filled donuts = 9 inch

So, diameter of each filled donuts =
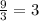`(9)/(3) = 3` inch and the radius
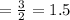`= (3)/(2)= 1.5` inch.

Area of each filled donuts =
`\pi r^2 = \pi (1.5)^2 = 2.25\pi` in²

So, the area covered by three filled donuts
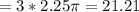`= 3*2.25\pi = 21.21` in²

2. Diameter of each glazed donuts = 3 in and diameter of each small circle inside = 1 in

So, the radius of each glazed donuts
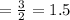`= (3)/(2)= 1.5` in and radius of each small circle
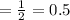`= (1)/(2)= 0.5` in

So, the area of each glazed donuts
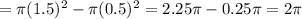`= \pi (1.5)^2 - \pi (0.5)^2 = 2.25\pi -0.25\pi = 2\pi` in²

The Area covered by three glazed donuts
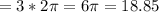`= 3* 2\pi = 6\pi = 18.85` in²

3. Total area covered by 6 donuts = 21.21 + 18.85 = 40.06 in²

Area of the box = (length) × (width) = (9 × 6)in² = 54 in²

So, the area of the bottom of the box (the shaded region) not covered by donuts = (54 - 40.06) in² = 13.94 in²