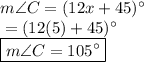Question

Quadrilateral ABCD is inscribed in a circle such that m∠A=(x2+50)∘ and m∠C=(12x+45)∘ .

What is m∠C ?

Enter your answer in the box.


plz explain what was done to get the answer

Answer 1

105

Step-by-step explanation: cuz I'm awesome

Answer 2

Answer: 105 degrees

Step-by-step explanation: In a quadrilateral that is inscribed in a circle, the opposite angles are supplementary. Since angle A and angle C are opposite angles, they are supplementary. In terms of equation,


`m \angle A + m \angle C = 180^(\circ) \\ \indent (x^2+50)^(\circ) + (12x+45)^(\circ) = 180^(\circ) \\ \indent (x^2 + 12x + 95)^(\circ) = 180^(\circ) \\ \indent x^2 + 12x + 95 = 180 \\ \indent x^2 + 12x - 85 = 0 \\ \indent (x - 5)(x + 17) = 0 \\ \indent \boxed{x = 5 \text{ or } x = -17}`

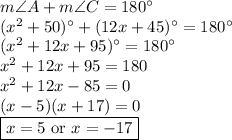
Note that if x = -17,


`m \angle C = 12x+45 \\ \indent = 12(-17) + 45 \\ \indent m \angle C = -159`

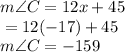
which is not valid because angle measure is not negative.

So, x = 5. Hence,


`m \angle C = (12x+45)^(\circ) \\ \indent = (12(5) +45)^(\circ) \\ \indent \boxed{m \angle C = 105^(\circ)}`