Answer:
1.09 square units.
Explanation:
The given curves are
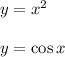
Let us plot the graph of these curves in the same coordinate axes. The graphs and the shaded region has been shown in the attached image.
The area of shaded region is given by

Now, we evaluate this definite integral to find the area of the shaded region.
![2\left [ \sin x-(x^3)/(3) \right ]_(0)^(0.824)\\\\2*(0.73386-0.18649)\\\\=2\cdot \:0.54737\\\\=1.09475](https://img.qammunity.org/2019/formulas/mathematics/college/oty6wnkeejkd85nzkllcijsgn7p2m0vgs2.png)
Therefore, the area of the region bounded by the given curves is 1.09 square units.