Question

Given the following functions f(x) and g(x), solve f[g(10)] and select the correct answer below:

f(x) = 10x + 8

g(x) = x + 9


A. 2,052

B. 98

C. 190

D. 198

Answer 1

g(10) = 10 + 9 = 19

f[g(10)] = 10(19) + 8 = 190 + 8 = 198

answer
D. 198

Answer 2

Option D is correct.

`f[g(10)]` = 198

Explanation:

Given the function:

`f(x) = 10x+8`

`g(x) = x+9`

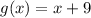
Solve:
`f[g(10)]`

First calculate:

f[g(x)]

Substitute the function g(x)

`f[x+9]`

Replace x with x+9 in the function f(x) we get;

`f(x+9) = 10(x+9)+8`

The distributive property says that:

`a\cdot (b+c) = a\cdot b+ a\cdot c`

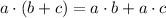
Using distributive property:

`f(x+9) = 10x+90+8=10x+98`

⇒
`f[g(x)] = 10x+98`

Put x = 10 we get;

`f[g(10)] =10(10)+98=100+98=198`

Therefore, the value of
`f[g(10)]` is 198