Question

Assume that women have heights that are normally distributed with a mean of 63.6 inches and a standard deviation of 2.5 inches. find the value of the third quartile q3.

round your answer to the nearest tenth.

Answer 1

The correct answer is:

65.3.

Step-by-step explanation:

Q3 is the third quartile, and represents 75% of the data. This means 75% of the data will fall below this value.

Using a z-table, we see that the z-score associated with a probability of 0.75 is between 0.67 and 0.68; we will use 0.675.

The formula for a z-score is:

`z=(X-\mu)/(\sigma)`,

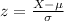
where X is our value, μ is the mean and σ is the standard deviation.

We know that z = 0.675; μ is 63.6; and σ is 2.5:


`0.675=(X-63.6)/(2.5)`

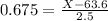
Multiply both sides by 2.5:


`0.675* 2.5=(X-63.6)/(2.5)* 2.5 \\ \\1.6875=X-63.6`

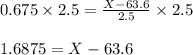
Add 63.6 to both sides:
1.6875+63.6 = X-63.6+63.6
65.2875 = X
65.3 ≈≈ X

Answer 2

we need to find α=Q3 such that P(z≤α)=0.75
From the standard table, we get
P(Z≤0.675)=0.75
thus
α=0.675
⇒[H-63.6]/2.5=0.675
solving for H we get
H-63.6=1.6875
hence
H=65.2875
The 3rd quartile is 65.2875