Answer:
C is correct. y=3x+14
Explanation:
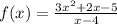
We need to find oblique asymtotes of f(x).
Oblique asymtotes form when degree of numerator is greater than denominator.
First we find the degree of numerator and denominator for f(x)
Degree of f(x) at numerator = 2
Degree of f(x) at denominator = 1
So, one oblique asymtote form.
First we divide
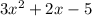 by
by
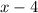
Quoetient of the above division would be oblique asymtote.
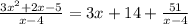
So, oblique asymtote would be y=3x+14
C is correct option.