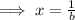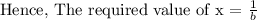Question

If (x, 0) lies on the graph of y = logbx, then x =

Answer 1

`\text{The required value of x = }(1)/(b)`

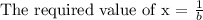
Explanation:

The function which is representing the graph is given to be : y = log (bx)

Now, as given the point (x,0) lies on the given graph

And if a point lies on a graph then the point satisfies the corresponding equation of the graph.

⇒ (x,0) satisfies the equation of the given graph.

⇒ (x,0) satisfies the equation : y = log (bx)

⇒ 0 = log (bx)

⇒ bx = 1

`\implies x=(1)/(b)`

`\text{Hence, The required value of x = }(1)/(b)`

Answer 2

We have the following expression:
y = logbx
We clear x of the expression.
We have then:
b ^ y = b ^ (logbx)
Rewriting:
x = b ^ y
Substituting we have:
x = b ^ 0
x = 1
Answer:
If (x, 0) lies on the graph of y = logbx, then:
x = 1