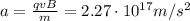Question

An electron of kinetic energy 45 keV moves in a counter-clockwise circular orbit perpendicular to a magnetic field of 0.325 T. Calculate the acceleration of the electron.

Answer 1

Let's convert the kinetic energy of the electron from keV to Joule:

`K=45 \cdot 10^3 eV \cdot 1.6\cdot 10^(-19) J/eV =7.2 \cdot 10^(-18)J`
And from the kinetic energy, we find the velocity of the electron:

`K= (1)/(2)mv^2`
where
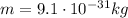
`m=9.1 \cdot 10^(-31) kg` is the electron mass. Re-arranging the formula, we find v:

`v= \sqrt{ (2K)/(m) } =3.98 \cdot 10^6 m/s`

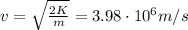
The magnetic force acting on the electron is:
F=qvB
where

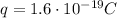
`q=1.6 \cdot 10^(-19) C` is the electron charge

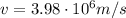
`v=3.98 \cdot 10^6 m/s` is the electron velocity
B=0.325 T is the magnetic field.

For Newton's second law, we also have that F=ma, so we can rewrite the equation as

`ma=qvB`
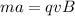
and so from this, we can find the acceleration (which is a centripetal acceleration, because the electron is moving by circular motion):

`a= (qvB)/(m)=2.27 \cdot 10^(17) m/s^2`