Question

What kinetic energy must alpha particles have in order to make contact with a mercury nucleus?

Answer 1

First, we need to approximate the size of a mercury nucleus. We will use the following formula:

`R=r_0A^{(1)/(3)}`
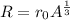
Where A is the atomic mass number and r_0 is the constant.
You can think of this as packing marbles of identical radius together. In that sense, r_0 would give you the approximation of the radius of a nucleon.
Atomic mass number of mercury is 201, and r_0 has a value of:

`r_0=1.25\cdot10^(-15) m`

`R=201^(1/3) \cdot 1.25\cdot10^(-15)=7.322\cdot 10^(-15)`
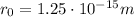
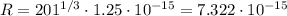
That gives us the radius of the outer shell of the nucleus of mercury. In order to "touch" the nucleus alpha particle must reach this shell. The amount of energy needed for this is simply the potential energy of the electric field.
This electric field has its origin in the center of the nucleus.
The potential energy in an electric field is given with:

`U_e=(qQ)/(k_er^2)`
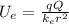
Where Q and q are the charges of interacting particles. We know that mercury has 80 protons and alpha particle has 2.

`U_e=(2\cdot80\cdot1.6\cdot10^(-19))/(8.98\cdot10^(9)\cdot7.322\cdot 10^(-15))\\ U_e=3.89\cdot10^(-13) J`