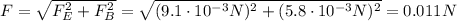Question

A magnetic field has a magnitude of 1.20 10-3 t, and an electric field has a magnitude of 5.70 103 n/c. both fields point in the same direction. a positive 1.8-�c charge moves at a speed of 3.00 106 m/s in a direction that is perpendicular to both fields. determine the magnitude of the net force that acts on the charge.

Answer 1

Let's take the x,y,z axis such that the electric field E and the magnetic field B are on the x-axis and the velocity of the particle is on the y-axis.

The charge is
`q=1.8 \mu C=1.8 \cdot 10^(-6) C`.

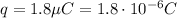
The electric force acting on the charge is

`F_E = qE=(1.6 \cdot 10^(-6) C)(5.7 \cdot 10^3 N/C)=9.1 \cdot 10^(-3) N`
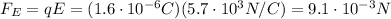
and the direction is the same as the electric field, so on the x-axis.

The magnetic force acting on the charge is

`F_B = qvB = (1.6 \cdot 10^(-6) C)(3 \cdot 10^6 m/s)(1.2 \cdot 10^(-3)T)=5.8 \cdot 10^(-3)N`
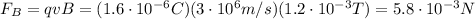
and by using the right hand rule, we find that the direction of the force is on the z-axis.

So, the two forces Fe and Fb are perpendicular to each other. Therefore, the net force acting on the particle is the resultant of the two forces:

`F= √(F_E^2+F_B^2)= \sqrt{(9.1 \cdot 10^(-3) N)^2+(5.8 \cdot 10^(-3)N)^2} =0.011 N`