Question

Find m∠A given ΔABC where a=4, b=6, c=3.

Answer 1

For this question, we're going to use the law of cosines.
The law of cosines is the following equation:


`a^2=b^2+c^2-2(b)(c) \cos(A)`

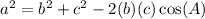
We know the values of a, b, and c. We want to find the measure of angle A.

`a=4`

`b=6`

`c=3`

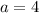
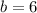
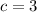
Now, plug in these values into the equation.


`4^2=6^2+3^2-2(3)(6) \cos(A)`

`16=45-36 \cos(A)`

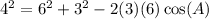
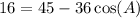
Add both sides by
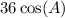
`36 \cos(A)` and subtract both sides by 16


`36 \cos(A)=29`

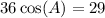
Divide both sides by 36


`\cos(A)= (29)/(36)`

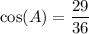
Take the inverse cosine, or arc cosine, of both sides.
Using a calculator, you'll get the following result.


`A \approx 36.3^O`

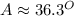
The measure of angle A should be 36.3 degrees. Hope this helps! :)