Question

Using the technique in the model above, find the missing segments in this 30°-60°-90° right triangle.

BC = 2

CD =

Answer 1

Answer: CD=
`√(3)`

Step-by-step explanation: We are given triangle ABC.

CD is a perpendicular line on AB.

< B = 60°

BC = 2 units.

We need to find the value of side CD.

In triangle BCD, we can see that <CDB is a right triangle, because CD is a perpendicular line on AB.

And <CBD = 60° that is given.

Therefore, < BCD = 30 degrees angle.

In order to find the value of CD, we can apply 30°-60°-90° right triangle rule to find the value of CD.

According to 30°-60°-90° right triangle rule adjacent side of 60° angle is half of Hypotenuse.

Therefore, BD = Half of BC = 2/2 = 1 unit.

And according to 30°-60°-90° right triangle rule opposite side is
`√(3)` times of adjacent side of 60° angle.

Therefore, CD = BD ×
`√(3)` = 1×
`√(3)` =
`√(3)`.

Therefore, CD =
`√(3)`.

Answer 2

Consider right triangle BCD: angle D is right and angle B has measure 60°, then angle C has measure 180°-90°-60°=30°. BC is the hypotenuse of this triangle. In special 30°-60°-90° right triangle the leg that lies opposite to the angle 30° is half of hypotenuse. So, BD=BC/2=2/2=1.

Consider right triangle ABC: angle C is right, angle B has measure 60° and angle A has measure 30°. AB is the hypotenuse of this triangle. In special 30°-60°-90° right triangle the leg that lies opposite to the angle 30° is half of hypotenuse. So, BC=AB/2, therefore AB=2BC=2·2=4 .

The hypotenuse AB consists of two parts: AD and BD. Since AB=4, BD=1, you have that AD=AB-BD=4-1=3.

The height of right triangle drawn to the hypotenuse is the geometrical mean of the previous parts:

`CD^2=AD\cdot BD,\\ CD^2=3\cdot 1=3,\\ CD=√(3)`.

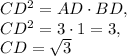Consider right triangle ACD: angle D is right and angle A has measure 30°, then angle C has measure 180°-90°-30°=60°. AC is the hypotenuse of this triangle. In special 30°-60°-90° right triangle the leg that lies opposite to the angle 30° is half of hypotenuse. So, CD=AC/2, AC=2·CD=2·√3=2√3.

Answer: AB=4 (hypotenuse), BD=1 and AD=3 (legs projections on the hypotenuse), CD=√3 (height to the hypotenuse), AC=2√3 and BC=2 (legs).