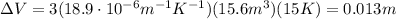Question

A silver cube has sides that measure 2.5 meters. The cube is heated from 15°C to 30°C. What is the change in its volume?

Answer 1

The initial volume of the silver cube is:

`V=(2.5 m)^3 = 15.6 m^3`

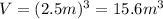
The volumetric thermal expansion of an object of volume V is given by
`\Delta V =3 \alpha _L V \Delta T`
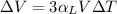
where
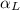
`\alpha_L` is the coefficient of thermal expansion and
`\Delta T` the temperature difference.
For silver,
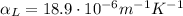
`\alpha_L = 18.9 \cdot 10^(-6) m^(-1)K^(-1)`, while the temperature difference in our problem is

`\Delta T = 30^(\circ)-15^(\circ)=15^(\circ)=15 K`
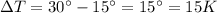
So we can calculate the change in volume of the silver cube:


`\Delta V = 3 (18.9 \cdot 10^(-6) m^(-1)K^(-1))(15.6 m^3)(15 K)=0.013 m`