Answer:
7 seconds
Explanation:
Given :
A baseball is thrown into the air from the top of a 224-foot tall building.
The baseball's approximate height over time can be represented by the quadratic equation
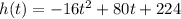
To Find: What is a reasonable time for it to take the baseball to land on the ground?
Solution:
Equation :
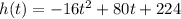
When factored this equation :
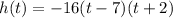 --A
--A
Now we are supposed to find reasonable time for it to take the baseball to land on the ground i.e. h =0
So, substitute h = 0 in A
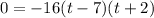
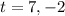
Since time cannot be negative
So, neglect -2
Thus it will taker 7 seconds for baseball to reach the ground.