Question

4 The ratio of corresponding dimensions of two similar solids is 3/4. The surface

area of the first solid is 96 m². Its volume is 720 m³. Find the surface area and
volume of the second solid. Round each answer to the nearest tenth, if
necessary. Show your work

5 A globe in a brass stand has a diameter of 40 in. What is the volume of the
globe to the nearest cubic inch? Show your work.

Answer 1

Question 4:

---------------------------------------------------
Ratio of Dimension to Area
----------------------------------------------------
Dimension : Area

`(3)/(4) \ : \ ((3)/(4) )^2`

`(3)/(4) \ : (9)/(16)`

---------------------------------------------------
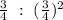
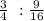
Find Area
----------------------------------------------------
Let x be the surface area of the second solid

`(9)/(16) = (96)/(x)`

`9x = 96 * 16`

`9x = 1536`

`x = 1536 / 9`

`x =170.7 m^2 (\ nearest \ tenth )`

---------------------------------------------------
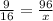
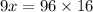
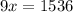
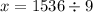
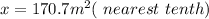
Answer: 170.7 m²
----------------------------------------------------


---------------------------------------------------
Ratio of Dimension to Volume
----------------------------------------------------
Dimension : Volume

`(3)/(4) \ : \ ((3)/(4) )^3`

`(3)/(4) \ : \ (27)/(64)`

---------------------------------------------------
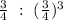
Find Volume
----------------------------------------------------
Let x be the surface are of the second solid

`(27)/(64) = (720)/(x)`

`27x = 720 * 64`

`9x = 46080`

`x = 146080 / 27`

`x =1706.7 m^2 (nearest \ hundredth )`

---------------------------------------------------
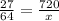
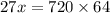
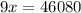
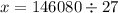
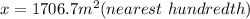
Answer: 1706.7 m³
----------------------------------------------------


Question 5
---------------------------------------------------
Find Radius
---------------------------------------------------
Radius = Diameter ÷ 2
Radius = 40 ÷ 2
Radius = 20

---------------------------------------------------
Find volume of the globe, which is a sphere
---------------------------------------------------

`Volume \ of \ sphere \ = (4)/(3) \pi x^(3)`


`Volume \ of \ sphere \ = (4)/(3) \pi (20)^(3)`


`Volume \ of \ sphere \ = 33510.3 in^3 \ ( \ nearest \ hundredth )`

---------------------------------------------------
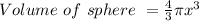
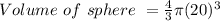
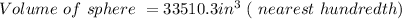
Answer: 33510.3 in³
----------------------------------------------------

Answer 2

4.

The ratio is 3/4 for corresponding dimensions, the ratio of their surface areas is equal to the square of this ratio:


`\sf ((3)/(4))^2=(S)/(96)`

Simplify the exponent:


`\sf (9)/(16)=(96)/(S)`

Cross multiply:


`\sf 9S=1536`

Divide 9 to both sides:


`\sf S\approx 170.7~m^2`

So the surface area of the second solid is 54 square meters.

The ratio is 3/4 for corresponding dimensions, the ratio of their volumes is equal to the cube of this ratio:


`\sf ((3)/(4))^3=(720)/(V)`

Simplify the exponent:


`\sf (27)/(64)=(720)/(V)`

Cross multiply:


`\sf 27V=46080`

Divide 64 to both sides:


`\sf V\approx 1706.7~m^3`

5.

A globe is a sphere, use the formula for the volume of a sphere:


`\sf V=(4)/(3)\pi r^3`

The radius is half of the diameter, so the radius here is 40/2 = 20. Plug it in the formula, use 3.14 to approximate for Pi:


`\sf V=(4)/(3)(3.14)(20)^3`

Simplify the exponent:


`\sf V=(4)/(3)(3.14)(8000)`

Multiply:


`\sf V\approx \boxed{\sf 33,493~in^3}`