Question

Please answer these 2 and please give an explanation so i can learn it. Thanks

Answer 1

Question (4):

---------------------------------------------------------------------
Formula
---------------------------------------------------------------------
a² + b² = c²

---------------------------------------------------------------------
Substitute the values and solve the unknown
---------------------------------------------------------------------
4² + 3² = c²
c² = 16 + 9
c² = 25
c = √25
c = 5

---------------------------------------------------------------------
Answer: 5 inches
---------------------------------------------------------------------


Question (5):

---------------------------------------------------------------------
Given information
---------------------------------------------------------------------
Area of a square = 25m²

---------------------------------------------------------------------
Find length
---------------------------------------------------------------------
Area of a square = Length x Length
Length² = 25
Length = √25
Length = 5m

---------------------------------------------------------------------
Find Diagonal
---------------------------------------------------------------------
a² + b² = c²
5² + 5² = c²
c² = 25 + 35
c² = 50
c = √50
c = 5√2 (Radical Form) or 7.07 (rounded to nearest hundredth)

---------------------------------------------------------------------
Answer: Diagonal = 7.07m
---------------------------------------------------------------------

Answer 2

4.

The formula for the diagonal of a rectangle is:


`\sf D=√(l^2+w^2)`

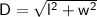
Plug in what we know:


`\sf D=√(4^2+3^2)`

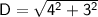
Simplify the exponents:


`\sf D=√(16+9)`

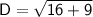
Add:


`\sf D=√(25)`

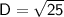
Take the square root:


`\sf D=\boxed{\sf 5~in}`

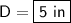
For the second one, we know that the area of a square is:


`\sf A=s^2`

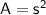
Plug in what we know:


`\sf 25=s^2`

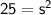
Take the square root of both sides:


`\sf s=5`

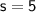
So we know that the length and width are both 5 meters long, let's plug this into the formula for the diagonal:


`\sf D=√(5^2+5^2)`

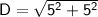
Simplify the exponents:


`\sf D=√(25+25)`

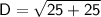
Add:


`\sf D=√(50)`

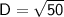
Take the square root:


`\sf D\approx\boxed{\sf 7.07~m}`