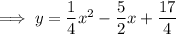Question

Write an

equation of a parabola with the given vertex and focus.
vertex (5,-2); focus (5, -1)

Answer 1

`(x-5)^2=4(y+2)`

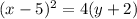
Please note that alternative forms of this equation (vertex and standard) are in the explanation.

Explanation:

Standard form of a parabola with a vertical axis of symmetry:

`\boxed{(x-h)^2=4p(y-k) \quad \textsf{where}\:p\\eq 0}`

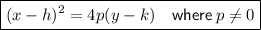
• Vertex = (h, k)
• Focus = (h, k+p)

Given:

• Vertex = (5, -2)
• Focus = (5, -1)

Therefore:

• h = 5
• k = -2
• k + p = -1

Calculate p:

`\implies -2+p=-1`

`\implies p=-1+2`

`\implies p=1`

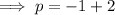
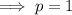
Substitute the values of h, k and p into the formula to create an equation of the parabola with the given parameters:

`\implies (x-5)^2=4(1)(y-(-2))`

`\implies (x-5)^2=4(y+2)`

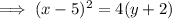
In vertex form:

`\implies y=(1)/(4)(x-5)^2-2`

In ax² + bx + c form:

`\implies y=(1)/(4)x^2-(5)/(2)x+(17)/(4)`