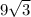Question

8. Find the value of x. If your answer is not an integer, leave it in simplest radical form. The diagram is not drawn to scale.

Answer 1

Here in the figure, a right angled triangle given.

One angle of other two angles given
`30^o`.

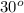The hypotenuse of an right angled triangle is always opposite to the right angle. So here, the side of length 18 is hypotenuse..

The side of length 9 is opposite to the ange given
`30^o`.

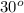So here two sides given and we need to find the third side.

We can get the third side by using either a trigonometric function or by using Pythagoras theorem.

Let's use Pythagoras theorem here.

We know the theorem is if a and b are other two sides and c is the hypotenuse then,
`c^2 = a^2+b^2`

Here, c = 18, and we can take b = 9 and a is x here. By substituting the values in the formula we will get,

`18^2 = x^2 + 9^2`

`324 = x^2+81`

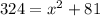
Now to get x, we will move 81 to the left side by subtracting it from both sides. We will get,

`324 - 81 = x^2+81-81`

`324-81 = x^2`

`243 = x^2`

`x^2 = 243`

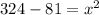
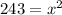
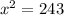
We acn get x by taking square root to both sides. We will get,

`√(x^2) = √(243)`

`x = √(243)`

We have to simplify 243 now. We can write 243 as a multiplication of 81 and 3.

`x = √((81)(3))`

`x = (√(81))(√(3))`

`x = 9√(3)`

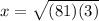
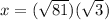
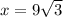
So we have got the required answer here. The side x =
`9√(3)`

Answer 2

x = 9 / tan(30)
x = 9 sqrt(3)