Find the critical points within the region:
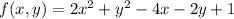

So (1, 1) is the only critical point of the function and it happens to fall within the rectangle

. At this point, we get a value of
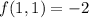
.
Now check along the boundaries for potential extreme values.
If

, then
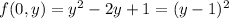
, which has a maximum when

and has a minimum when
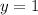
. So we have a potential extrema at
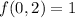
and
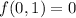
.
If
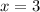
, then
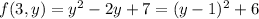
, with a max when

and min when
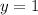
. So we have
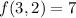
and
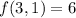
.
If
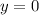
, then
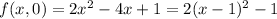
, with a max when
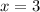
and a min when

. So we have
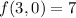
and
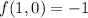
.
If

, then

again, with a max when
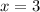
and a min when

. So we have, again,
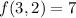
and
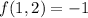
.
So there are absolute maxima of 7 at (3, 0) and (3,2), and an absolute minimum of -2 at (1, 1).