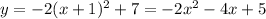Question

Determine the equation for the parabola graphed below.

Answer 1

The equation for the parabola graphed below is
`y = -2(x + 1)^2 + 7 = -2x^2 - 4x + 5`

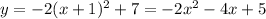
A parabola's general equation is: y = a(x - b)2 + c

Given that the vertex is located at (-1, 7), this means that b = -1 and c = 7:

y = a(x + 1)^2 + 7

Then, instead of the vertex, we replace a point from the graph. The y-intercept of (0, 5) is the simplest:

5 = a(1)^2 + 7

a = -2

As a result, the equation is as follows:
`y = -2(x + 1)^2 + 7 = -2x^2 - 4x + 5`

Answer 2

The general equation for a parabola is: y = a(x - b)^2 + c
So given the vertex is at (-1, 7), this means that b = -1 and c = 7:
y = a(x + 1)^2 + 7
Then we substitute a point from the graph (aside from the vertex). The easiest is the y-intercept of (0, 5):
5 = a(1)^2 + 7
a = -2
Therefore the equation is: y = -2(x + 1)^2 + 7 = -2x^2 - 4x + 5