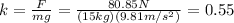Question

A sled of mass 15 kg slides across the ground with a friction force of 80.85 N. What is k between the sled and the ground?

Answer 1

0.55 is correct - APEX

Answer 2

The expression for the frictional force between the sled and the ground is:

`F=k m g`
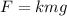
where
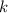
`k` is the coefficient of friction, m is the mass of the object and
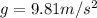
`g=9.81 m/s^2` is the gravitational acceleration.

The friction force in our problem is F=80.85 N. The mass of the object is m=15 kg. Re-arranging the formula, we can find the value of k:

`k= (F)/(mg)= (80.85 N)/((15 kg)(9.81 m/s^2))=0.55`