First we need to find what kind of sequence we have. To do that we are going to test if the sequence as a difference
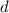
, in which case it will be an arithmetic sequence, or a ratio

, in which case it will be geometric sequence.
The formula to find
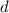
is
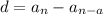
where
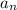
is the current term in the sequence
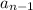
is the previous term in the sequence
The formula to find

is
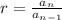
where
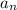
is the current term in the sequence
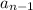
is the previous term in the sequence
- For
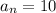
and
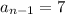
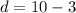
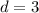
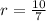
- For
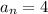
and
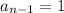
:
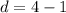
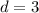
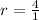
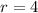
Since
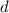
is equal in both procedures whereas

is not, we can conclude that our sequence is an arithmetic sequence.
Now we are going to use the explicit formula of an arithmetic sequence
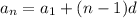
where
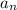
is the nth term
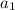
is the first term

is the position of the term in the sequence
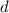
is the difference
We know that
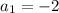
and
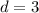
, so lets replace those values in our formula:
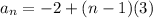
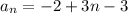
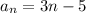
We can conclude that the correct answer is
D) an = 3n - 5