The given quadratic function is:
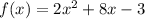
The zeros of the quadratic functions also known as its roots can be found using the quadratic formula.
According to the quadratic formula:
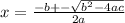
here,
b = coefficient of x-term
a = coefficient of x²-term
c = costant term
For given function:
a = 2
b = 8
c = - 3
Using these values in the formula, we get:
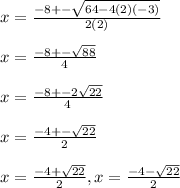
Thus, these values of x are the zeros of the given quadratic function f(x)=2x²+8x-3