Question

What is the sum of the geometric series

Answer 1

Which one theres many!! :)

Answer 2

Hence, the sum of the geometric series is:

259

Explanation:

We are given a geometric series as:

`\sum_(i=1)^4 6^(i-1)`

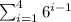
i.e. we are asked to fnd the sum of first four terms of the geometric series with first term as 1

Since, the series is:

`6^0+6^1+6^2+6^3`

Also, the common ratio of the series is: r=6

Since, each of the term of the series is 6 times it's preceding term.

Also we know that sum of a finite geometric series with n-terms and common ratio r is calculated by the formula:

`S_n=a((r^n-1)/(r-1))`

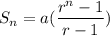
Here we have: a=1 and r=6 and n=4

Hence,

`S_4=1((6^4-1)/(6-1))\\\\\\S_4=(1295)/(5)\\\\\\S_4=259`

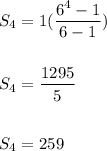
Hence, the sum of the series is:

259