Question

Scientists want to place a 3700 kg satellite in orbit around mars. they plan to have the satellite orbit a distance equal to 1.9 times the radius of mars above the surface of the planet. here is some information that will help solve this problem: mmars = 6.4191 x 1023 kg rmars = 3.397 x 106 m g = 6.67428 x 10-11 n-m2/kg2 1) what is the force of attraction between mars and the satellite?

Answer 1

3805.59 N

Step-by-step explanation:

Parameters given:

Mass of satellite, m = 3700 kg

Mass of Mars, M =
`6.4191 * 10^(23) kg`

Radius of Mars, r =
`3.397 * 10^6` m

Distance between the satellite and the surface of Mars, D = 1.9 times r

D =
`1.9 * 3.397 * 10^6` =
`6.454 * 10^6 m`

The gravitational force of attraction is given as:

`F = (GMm)/(D^2)`

where G = gravitational constant =
`6.67428 * 10^(-11)Nm^2/kg^2`

`F = (6.67428 * 10^(-11) * 6.4191 * 10^(23) *3700)/((6.454 * 10^6)^2)`

`F = 3805.59 N`

The gravitational force of attraction is 3805.59 N

Answer 2

The force of attraction between Mars and the satellite is:

`F=G (Mm)/(d^2)`
where G is the gravitational constant, M the mass of Mars, m the mass of the satellite, and d the distance of the satellite from the center of Mars.

First we have to calculate d. Calling r the radius of Mars, we know that the satellite is located at 1.9r above the surface. This means that its distance from the center of Mars is
`d=1.9r +r=2.9 r`.
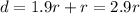
Using this information, and the data given by the problem, we can now calculate the intensity of the gravitational attraction:

`F=G (Mm)/((2.9r)^2)=(6.67 \cdot 10^(-11)Nm^(-2)kg^(-2)) ((6.42\cdot 10^(23)kg)(3700kg))/((2.9\cdot3.39 \cdot 10^6m)^2)=1639 N`