Question

Determine how many, what type, and find the roots for f(x) = x4 + 21x2 − 100.

Answer 1

Explanation:

We will make a substitution to make our work easier (when we get there). We also need to know that

`i^2=-1`

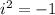
We will use that as another substitution. First, let's make the job of factoring a bit easier. Here's the first substitution. We will let

`x^4=u^2`

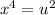
Therefore,

`x^2=u`

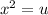
Now we will write the polynomial in terms of u instead of x:

`f(x)=u^2+21u-100`

Solve for the values of u by setting the polynomial equal to 0 and factoring. When you factor, you will get:

`(u+25)(u-4)`

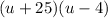
But don't forget that

`x^2=u`

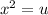
so we have to put those back in now:

`(x^2+25)(x^2-4)=0`

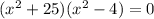
By the Zero Product Property, either

`x^2+25=0` or

`x^2-4=0`

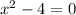
We will factor the first term. Solving for x-squared gives us:

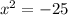`x^2=-25` and

x = ±√-25

which simplifies down to

x = ±√-1 × 25

we can sub in an i-squared for the -1:

x = ±√
`i^2*25`

The square root of i-squared is "i" and the square root of 25 is 5, so

x = ±5i

The next one is a bit easier. If

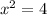`x^2=4`, then

x = ±2

You can see you have 4 solutions. But you knew that already, since this is a 4th degree polynomial. The types of solutions are: 2 real, 2 imaginary