Question

Write an equation for the intervals of a parabola with x-intercepts at (2,0) and and (-5,0) that passes through the point (1, -18).

Help is always greatly appreciated.

Answer 1

`\quad \huge \quad \quad \boxed{ \tt \:Answer }`

`\qquad\displaystyle \tt \rightarrow \: y= 3 {x}^(2) + 9x - 30`

____________________________________

`\large \tt Solution \: :`

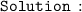
The values of x where a parabola cuts the x - axis (y = 0) are the roots of the quadratic equation.

I.e -5 and 2 for the given problem.

and the equation can be represented as :

`\qquad\displaystyle \tt \rightarrow \: y = a(x - x1)(x- x2)`

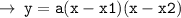
where, x1 and x2 are the roots of the quadratic equation, a is a constant value (depicting strech in curve)

Now, plug in the values :

`\qquad\displaystyle \tt \rightarrow \: y= a(x- 2)(x - ( - 5))`

`\qquad\displaystyle \tt \rightarrow \: y = a(x- 2)(x+ 5)`

`\qquad\displaystyle \tt \rightarrow \: y = a( {x}^(2) + 5x - 2x - 10)`

`\qquad\displaystyle \tt \rightarrow \: y= a( {x}^(2) + 3x - 10)`

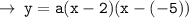
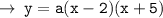
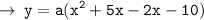
Now, we need to find the value of a, for that let's use the coordinates of a point lying on the curve (1 , -18)

`\qquad\displaystyle \tt \rightarrow \: - 18 = a( {1}^(2) + 3(1) - 10)`

`\qquad\displaystyle \tt \rightarrow \: - 18 = a(1 + 3 - 10)`

`\qquad\displaystyle \tt \rightarrow \: - 18 = a( - 6)`

`\qquad\displaystyle \tt \rightarrow \: a = ( - 18) / ( - 6)`

`\qquad\displaystyle \tt \rightarrow \: a = 3`

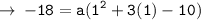
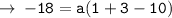
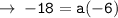
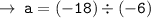
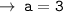
Now, we got all required values. let's plug the value of a in equation, and we will get the required equation of parabola.

`\qquad\displaystyle \tt \rightarrow \: y= 3( {x}^(2) + 3x - 10)`

`\qquad\displaystyle \tt \rightarrow \: y= 3 {x}^(2) + 9x - 30`

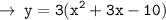
Answered by : ❝ AǫᴜᴀWɪᴢ ❞

Answer 2

`\textsf{Factored form}: \quad f(x)=3(x-2)(x+5)`

`\textsf{Standard form}: \quad f(x)=3x^2+9x-30`

Explanation:

Factored form of a quadratic function

`f(x)=a(x-p)(x-q)`

where:

• p and q are the x-intercepts.
• a is some constant.

Given x-intercepts:

• (2, 0)
• (-5, 0)

Substitute the given x-intercepts into the formula:

`\implies f(x)=a(x-2)(x+5)`

To find a, substitute the given point (1, -18) into the equation and solve for a:

`\implies -18=a(1-2)(1+5)`

`\implies -18=a(-1)(6)`

`\implies -6a=-18`

`\implies a=3`

Therefore, the equation of the function in factored form is:

`\boxed{ f(x)=3(x-2)(x+5)}`

Expand the brackets:

`\implies f(x)=3(x^2+3x-10)`

`\implies f(x)=3x^2+9x-30`

Therefore, the equation of the function in standard form is:

`\boxed{f(x)=3x^2+9x-30}`