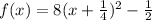Answer:
Vertex form:
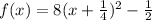
Explanation:
Given:
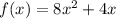
We need to write in vertex form.
Vertex form:
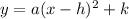
vertex: (h,k)
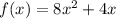
Step 1: Take out 8 common from each term
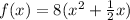
Step 2: Add and subtract square of half of coefficient of x
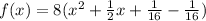
Step 3: Factor the term inside parentheses
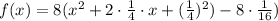
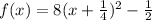
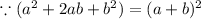
Hence, The vertex form of f(x)