Question

"A circuit consists of a battery and two resistors connected in parallel. If the resistance in both resistors is doubled, and the current is kept constant, how does the voltage change?"

Why is the voltage doubled?,

Answer 1

If the resistance in both resistors is doubled, then voltage gets doubled.

Step-by-step explanation:

It is given that, A circuit consists of a battery and two resistors connected in parallel.

In parallel combination of resistors the potential difference remains the same while the current divides. The equivalent resistance is given by :

`(1)/(R_(eq))=(1)/(R_1)+(1)/(R_2)`

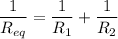
Initial condition, Let R₁ = R₂ = R

So,
`(1)/(R_(eq))=(1)/(R)+(1)/(R)`

`{R_(eq)=(R)/(2)`

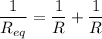
Using Ohm's law,

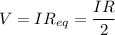`V=IR_(eq)=(IR)/(2)`...............(1)

Final condition, If the resistance in both resistors is doubled, and the current is kept constant.

So,
`(1)/(R'_(eq))=(1)/(2R)+(1)/(2R)`

`{R'_(eq)=R`

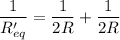
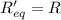
Voltage,
`V'=IR'_(eq)=IR`............(2)

From equation (1) and (2),

`V'=2V`

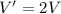
So, the new voltage gets doubled. Hence, this is the required solution.

Answer 2

Let's call R the value of the resistance of the two resistors. In the first situation, the resistors are connected in parallel, so their equivalent resistance is given by:

`(1)/(R_(eq))=(1)/(R)+(1)/(R)=(2)/(R)`
which means:

`R_(eq)=(R)/(2)`
And calling I the current in the circuit, the voltage is given by Ohm's law:

`V=IR_(eq)=(IR)/(2)`

In the second situation, the resistance of each resistor is doubled: R'=2R. So, the equivalent resistance in this case is given by

`(1)/(R_(eq))=(1)/(2R)+(1)/(2R)=(2)/(2R)=(1)/(R)`
which means

`R_(eq)=R`
And the new voltage is given by:

`V'=IR_(eq)=IR=2V`
which is twice the original voltage, so the voltage has doubled.