Answer:
The new radius of the balloon is 17.8 cm.
Step-by-step explanation:
Initial pressure of the air in the balloon =
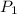 1.0 atm
1.0 atm
Radius of the balloon ,r= 17 cm
Volume of the spherical volume balloon =
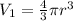
Final pressure of the air in balloon =
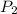 =0.87 atm
=0.87 atm
Radius of the balloon be R
Volume of the balloon be =
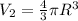
New radius of the balloon= R
According Boyle's Law:
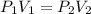
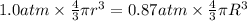
R =17.80 cm
The new radius of the balloon is 17.8 cm.